Glideevne C130 Hercules

[Miraculix]

Hei

Er ny på forumet og gleder meg til å lese gjennom postene her, er veldig flyinteressert.

Så til spørsmålet, vi satt en gjeng og pratet om forsvarets C130 og en av deltakerne påstod at hvis maskinen hadde maks marsjhøyde og fart så kunne den, hvis alle fire motorene kuttet over Danmark glidefly helt inn til Gardermoen, er dette virkelig mulig?
Har hørt også tidligere at maskinen er konstruert for å glidefly lengre distanser, men fra Danmark til Gardermoen er kanskje noe i overkant?

Mvh
Miraculix

 

[CFM]

Glidefly lengre distanser med Hercules? Aldri hørt om. Fra nordspissen av Danmark er det rundt 150 nautiske til Gardermoen. Hvis Herc'en cruiser på 28000 fot vil jeg si nei, det klarer den ikke. Kanskje en tredjedel av distansen på unten for mye vind.

 

[Wahoo]

CFM har rett, det er nok lite sannsynlig.

Hvis vi bruker eksempelet til CFM (Skagen-OSL) så vil avstanden være 150nm, høyden 4,6nm.
Det betyr en glideratio på 150/4,6 = 32,5 for å nå fram.

Ett glidefly har L/D ratio på mellom 30-50, ett passasjer/transportfly typisk 15-20, ett GA mellom 10-15.
Så Herc'en ville nok endt i sjøen i nærheten av Færder fyr..

 

[Miraculix]

Takk for svar, og kjøper absolutt disse.

Men for å være helt sikker, før jeg setter kompisen til veggs; Er dette regnestykket tatt med utgangspunkt i maks marsjhøyde som i følge Wikipedia er 40 000 fot?

 

[CFM]

Takk for svar, og kjøper absolutt disse.

Men for å være helt sikker, før jeg setter kompisen til veggs; Er dette regnestykket tatt med utgangspunkt i maks marsjhøyde som i følge Wikipedia er 40 000 fot?

40000 er ikke noen marsjhøyde for C-130. Jeg tok utgangspunkt i en service ceiling ppå 28000. Men fra 40000 trenger du fortsatt et glidetall på 22 og det tviler jeg sterkt på at du klarer med mindre du har en solid medvind.

 

[Miraculix]

Så med utgangspunkt i 40000 fots høyde, solid medvind og ellers optimale forhold så er det en liten mulighet for at dette går?

Kanskje gi ham delvis rett da?

 

[CFM]

Jeg ville sagt nei, men jeg har ikke noen eksakte tall for glidetallet for en C-130, men om vi skulle tatt et glidetall på 12:1 så ville du klart rundt 80NM uten vind. Hvis vi sier at du klarer å holde 1000 fpm descend rate tar det 40 min før du er nede. Da trenger du i snitt 105 knop medvind for å komme fram og det er før du har satt ut hjul og flaps.

 

[Miraculix]

Ok, Takk for svar

 

[CFM]

Bare hyggelig. Sett han til veggs med mindre han har bevis for at en Hercules glir bedre enn et rutefly

 

[LNv22]

CFM har rett, det er nok lite sannsynlig.

Hvis vi bruker eksempelet til CFM (Skagen-OSL) så vil avstanden være 150nm, høyden 4,6nm.
Det betyr en glideratio på 150/4,6 = 32,5 for å nå fram.

Ett glidefly har L/D ratio på mellom 30-50, ett passasjer/transportfly typisk 15-20, ett GA mellom 10-15.
Så Herc'en ville nok endt i sjøen i nærheten av Færder fyr..

Har et GA fly så dårlig glideevne? Faller en C 172 som en sten i forhold til en 737 uten motor?

 

[bamseh]

Har et GA fly så dårlig glideevne? Faller en C 172 som en sten i forhold til en 737 uten motor?

Ved å trimme en C172 til "maks glide" 65 kts IAS, så regner jeg som tommelfingerregel 500ft og 1 NM per minutt (i null-vind selvfølgelig).
Det skulle vel bli ca 11:1.

O'Store Google påstår at B737 ligger i overkant av 20:1, så..

 

[LNv22]

Ved å trimme en C172 til "maks glide" 65 kts IAS, så regner jeg som tommelfingerregel 500ft og 1 NM per minutt (i null-vind selvfølgelig).
Det skulle vel bli ca 11:1.

O'Store Google påstår at B737 ligger i overkant av 20:1, så..

Det vil da si at du i 65 knop kommer deg 1 NM pr. minutt og bare mister 500 ft pr. minutt?

Hvis man da flyr i 8000 fot gir det hele 16 minutter til å glidefly ned til et eller annet sted å sette ned maskinen?

 

[bamseh]

C172

Det vil da si at du i 65 knop kommer deg 1 NM pr. minutt og bare mister 500 ft pr. minutt?

Hvis man da flyr i 8000 fot gir det hele 16 minutter til å glidefly ned til et eller annet sted å sette ned maskinen?

Grovt regnet, ja. Jeg kan forøvrig love deg at jeg bruker minst 10-12 av de minuttene på å prøve å starte motoren igjen

Avstanden vil variere med vinden, med 30 kt motvind vil man jo bare oppnå 0,5 NM, og med 30 kt medvind får du 1,5 NM.

Den praktiske bruken av denne informasjonen kan være hvis du f.eks. er over hav - vil det lønne seg å fortsette fremover eller snu og fly tilbake?
Si du er i 2000 ft, og det er 2 NM til land fremover med de nevnte 30 kts motvind, og 4 NM "bakover". Fortsetter du fremover vil du "akkurat nå land" (eller ikke) etter 4 minutter - men snur du flyet vil du være over land etter knappe 3 minutter, og fremdeles ha et minutt "til gode" i lufta...

Så var det det å være kald nok til å velge å fly 4 NM over vannet fremfor 2 NM uten motordur...

 

[Wahoo]

O'Store Google påstår at B737 ligger i overkant av 20:1, så..

Google er nok noe optimistisk, NG ligger såvidt jeg vet rundt 17-18 og CL 16-17.
Winglets øker L/D noe - som sikkert noen piloter her kan bekrefte - at de trenger ett par nautiske mil ekstra (evt mer speedbrake) for
å få kjerra ned på bakken.

W

 

[Wahoo]

Fant forøvrig fasiten for for C130 Hercules.
L/Dmax = 19,5
Med vingetanker, ca 17,5.

Så den er nok sjanseløs å nå OSL

W

 

[Miraculix]

Fant forøvrig fasiten for for C130 Hercules.
L/Dmax = 19,5
Med vingetanker, ca 17,5.

Så den er nok sjanseløs å nå OSL

W

Kjempemessig :thumbup

Skjønner ikke så mye av diagrammet selv, men hvor langt ville det være mulig å glidefly når utgangspunktet er motorkutt over Skagen i 40000 fot og optimale vindforhold? Når vi en flyplass i Norge, eller snur vi og lander i Danmark?

Litt artig å kunne dokumentere skikkelig når en skal sette noen til veggs.

 

[Dag Johnsen]

Heisan Miraculix!

Skjønner ikke så mye av diagrammet selv, men hvor langt ville det være mulig å glidefly når utgangspunktet er motorkutt over Skagen i 40000 fot og optimale vindforhold?

Ja, men du kan da regne? Som Whahoo sin graf beskriver vil hele flyet produsere drag og noe loeft, saa forholdet mellom loeft og drag (L/D) er gitt for hele flyet. Glidetallet, som er er forholdet mellom et fly uten thrust sin bevegelse framover til synketallet ved en bestemt fart, det samme tallet som L/D. Du kan da regne fra hoyden av flyet, gjoer om fra fot til Km og regn ut fra glidetallet, saa finner du straks ut hvor langt flyet gaar.

Dag

 

[rymle]

Skjønner ikke så mye av diagrammet selv, men hvor langt ville det være mulig å glidefly når utgangspunktet er motorkutt over Skagen i 40000 fot og optimale vindforhold? Når vi en flyplass i Norge, eller snur vi og lander i Danmark?

40,000ft for en C130 er urealistisk. Bruk heller 30,000.

 

[Wahoo]

Skjønner ikke så mye av diagrammet selv,

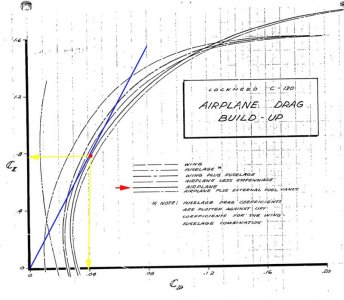
Diagrammet viser sammenhengen mellom Cl (løft) og Cd (drag) for C130 Hercules.
Dette er ett av de viktigste design parameterene for ett fly.
L/D ratio betyr forholdet mellom Cl og Cd, den ene delt på den andre. Jo høyere L/D ratio er jo mer
effektiv er vingen. Glidere har som vi vet en veldig effektiv vinge, en vinge hvor man får mye løft og
har lite drag. De trenger altså veldig lite motorkraft for å holde seg i luften og klarer seg faktisk med termiske luftstrømmer.
Så hvorfor lager man da ikke passasjerfly/transportfly med veldig høy L/D? Hovedårsaken er at disse vingene
ikke tåler særlig høy fart, og ellers er veldig upraktiske på en flyplass da de må være veldig lange og tar mye plass.

For å finne L/D max på kurven, så trekker man en linje (blå) roterende rundt origo (0,0) og lar den tangere (berøre)
den kurven man ønsker (den markert med rød pil). Dette tangeringspunktet er L/D max (rød prikk).
Så leser vi av på aksene (gult) og får omtrent Cl = 0,78 og Cd = 0,041. L/D max = 0,78/0,041 = 19,0.

Alle andre punkter på den kurvede Cl/Cd linjen vil ha en lavere L/D ratio (Cl/Cd).

Løft og drag er avhengig av hvilken vinkel vingen har mot luftstrømmen i fartsrettningen (AoA - angle of attack).
Jo høyere vinkel, jo høyere drag og løft (helt til vingen steiler). Så man kan si at jo høyere Cl er jo høyere AoA.
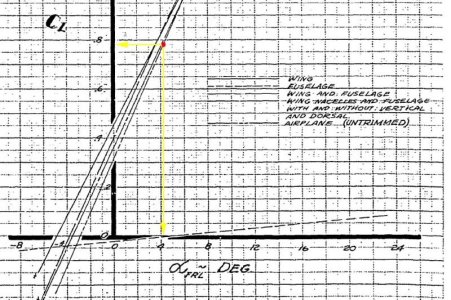
Vi fant at Herculesen var mest effektiv ved Cl = 0,78. Har en annen graf som viser at for Cl 0,78 så gir
det en optimal AoA (Alpha) på ca 4,1 grader for Hercen (vedlagt)

Tenk deg at en Herc cruiser med konstant fart (med motor) med AoA = 4,1 grader. Tenk deg så at du hiver oppi noen tonn ekstra vekt.
Hva skjer? Jo AoA (pitch) må øke for at flyet skal klare å beholde høyden (øke løftet). Flyet har med andre ord fått en høyere AoA og har blitt mindre effektiv.
For å komme seg tilbake til optimale AoA = 4,1 grader må piloten altså fly fortere for å få senket nesen tilbake til 4,1 grader.
Ett annet alternativ er å gå ned til en lavere høyde hvor løftet er større. Vekten påvirker altså ikke L/D maks, men ett tungt fly
må fly raskere eller lavere for å være like (aerodynamisk) effektivt.

W